Profile
Thomas Woolley
Curriculum Vitae
-
Education:
Leys Junior School (Alfreton, Derbyshire), Mortimer Wilson Secondary School and Sixth form (Alfreton, Derbyshire), University of Oxford, St John's College (Oxford, Oxfordshire)
-
Qualifications:
GCSE: 6A*, 4A and a B (in music :(). A Levels: A in Maths, Further Maths, Physics and Chemistry. MMath: First. Doctorate: Pass with minor corrections.
-
Work History:
Dining Room Attendant. Maths advisor of TV shows. Fellow of Modern Mathematics for the London Science Museum. Online maths tutor. Lecturer.
-
Current Job:
Senior Lecturer at Cardiff University
-
Employer
Cardiff University
-
About Me
Mathematical Biologist producing beauty from numbers
-
Read more
I studied mathematics at University of Oxford between 2004-2017 and I am now a Senior Lecturer in Applied Mathematics in Cardiff University. During my education I took a class in mathematical biology and fell instantly in love. I followed this direction and ended up doing a doctorate focused on understanding the pattern formation behind fish spots and zebra stripes. Alongside this research I now investigate mathematical models of stem cell movement, organ growth and IVF optimisation.
My hope is that by understanding the biological systems better through mathematics we can influence them and make them better.
When not doing mathematics, I am a keen participant in mathematical outreach workshops and I have given a variety of popular maths lectures nationally and internationally. I have previously worked for the BBC, illustrated Marcus du Sautoy’s book and worked on the popular maths show “Dara O’Briains school of hard sums”. Most recently I was the Fellow of Modern Mathematics at the London Science Museum and helped redesign their mathematics gallery.
Alongside these project I host, edit and produce a podcast called “Maths at”.
Originally, it was just an audio podcast where I and my co-hosts discussed mathematical movies
https://podcasts.apple.com/gb/podcast/maths-at/id1282043127
Now we’ve ascended into videos and discuss mathematics appearing in the news
-
How I Use Maths In My Job:
Being a mathematical lecturer I use mathematics every day of my life!
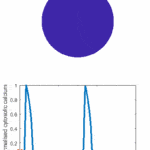
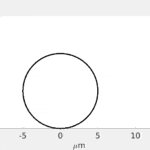
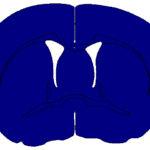
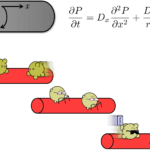
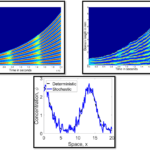
Specifically, I use “partial differential equations” to model developing biological systems. Although they sound complex, these equations are just rigorous ways of writing down our biological knowledge. I then simulate these equations and try to reproduce reality.
Click on one of the images in the gallery to see the animations that I produce. Can you tell what each of is meant to be?
-
My Work
PATTERNS!
-
Read more
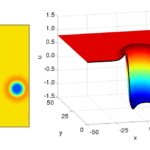
My research focuses on understanding how biological systems develop patterns. Critically, when I say pattern, this can mean any complicated spatial structure, from finger digit formation, to stripes on zebras.
The theory dates back to 1952, when Alan Turing published the ground-breaking paper “On the chemical basis of morphogenesis”. A complicated title, but essentially it asks: how does structure form from very simple origins? Namely, the biochemicals that allow embryos to develop have no understanding of the structure that they are producing, yet, with unerring robustness we reproduce with few errors.
The theory was highly counter intuitive for the time that it was produced. Specifically, the theory demonstrates that diffusion can generate patterns. This should seem very peculiar because diffusion is just the description of microscale random movement. For example, if you put red ink in water and neither stir, nor heat the liquid, the ink will still spread out slowly. Over time diffusion spreads the ink throughout the water, producing a uniform red water colour. Critically, no pattern is produced. However, Turing’s theory demonstrated that diffusion, which normally wiped patterns out, could in fact be used to create patterns.
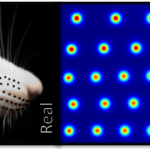
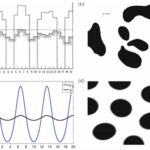
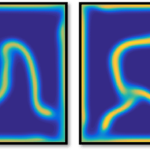
Although Turing was ahead of his time in many ways, he was greatly limited by the power of computers that he was helping to develop. Figure 1 demonstrates the simulations that he could achieve in his time compared to what we can achieve now. We can even go much further than Turing ever could and present all general patterns that can be found. Namely, Turing patterns all come in one of three varieties, spots, stripes, or labyrinthine.
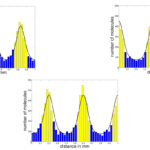
Since Turing’s original paper there have been a huge number of extensions allowing us to better understand potential limitations in biology. For example, the patterns that are produced are heavily dependent on the size of space we are working on. Specifically, as space gets smaller the patterns should get simpler, going from spots, to stripes, to nothing. Now, although certain animals do illustrate this spatial dependence in their patterning, others do not. There are many reasons why a lemur may not be described by the same theory as a cheetah, but safe to say such patterning restrictions allow us to separate out those animals whose patterns may be Turing patterns and those that probably are not.
Another insight concerning size and patterning is that as the skin gets larger the pattern should go through specific transitions. Namely, as the skin gets larger, the first pattern we see should be binary one. Namely, one half of the animal should be one colour and the other half should be a different colour, this is seen in the case of the Valais goat. However, as the skin gets larger, we transition to the point of having three patterning regions, which can be compared with the Belted Galloway cow. Amazingly, as predicted by the mathematics. The goat is approximately 40% of the size of the cow.
-
My Typical Day
Sleep - Zoom meeting - Eat - Zoom meeting - Sleep
-
Read more
My typical day involves lecturing students on a range of applied mathematics topics, doing my own research and supervising graduate students.
Normally, I’d be doing these things from inside Cardiff’s School of Mathematics (see the video), but due to the corona virus all of teaching and supervisions have gone online. It’s not a huge barrier to my work because theoretical mathematics can be done anywhere, but I do miss the interpersonal feedback you get from being in the same room as other people.
-
What I'd do with the prize money
By new equipment for my podcast.
-
Read more
As mentioned above I edit, host and produce a podcast on the mathematics appearing in the news. We’ve been recording audio and video using out tablets, laptops and phones. However, it’d be great to actually have some proper equipment to make the quality better.
-
My Interview
-
What or who inspired you to follow your career?
My secondary school maths teacher and my university lecturers.
What's your favourite use for maths in everyday life?
Producing beautiful patterns.
What did you think about Maths when you were in school?
It offered a correct way to think.
What did you want to be after you left school?
Taller
Were you ever in trouble at school?
N'ah, I was the academic kid who followed the rules.
If you weren't doing this job, what would you choose instead?
Teaching
Who is your favourite singer or band?
Queen
What's your favourite food?
Carrot cake
What is the most fun thing you've done?
I got to go on a zombie survival today
If you had 3 wishes for yourself what would they be? - be honest!
I would love the ability to manipulate time: slow it down, speed it up, etc. I wish mathematics and the sciences more broadly always had as much funding as it needed. I wish my daughter could grow up without fearing global climate change.
Tell us a joke.
I got my friend a telepathic abacus for her birthday. It's the thought that counts!
-